本当に苦手なのはなんなのか
木曜、朝から身体が重い。いつもより遅めの8:30出社。10:30〜沖縄チームと打合せ。まもなくたくさんのプロジェクトが一...
お便りフォーム
P.S.
ピーエス
2026年2月6日
気になってしまった木曜
木曜、締切（ダブル）前日で諸々の作業に追われる。
が、気になってしょうがなかったのでつい0.066%について調べてしまう。とはいえ手計算でちまちまやってる暇はないのでgeminiに聞いてみる。
まず、「8人の人間がいる時、その中に少なくとも1組の同月同日生まれがいる可能性は？」
聞いたらすぐに「誕生日のパラドックスですね」と返してくる。それは私も知っている。確率計算と直感のギャップの話。よく例に挙げられるのは「サッカーの両チーム、審判1名の合計23名で少なくとも1組の同じ誕生日が存在する確率は？」というものでこれが50%を超えるという話。
で、さっきの問いの答えは【7.43％】
続いてこう聞く「では8人のうち、2組の同じ誕生日がいる確率は？」
答えは【0.22%】
さて、いよいよ本題。
「では8人という人数は同じだけど、4人のグループが2つある時、同じグループ内での同じ誕生日は除外したうえで同じ誕生日が2組存在する確率は？」
するとgeminiが条件を整理してくれて、
なるほど、非常に面白いパズルですね！条件を整理すると以下のようになります。
グループA（4人）：メンバー同士の誕生日は全員違う。
グループB（4人）：メンバー同士の誕生日は全員違う。
求めたい状況：グループAの誰かとグループBの誰かが同じ誕生日、というペアがちょうど2組成立する確率。
そうそう、そういうこと。で、答えは？
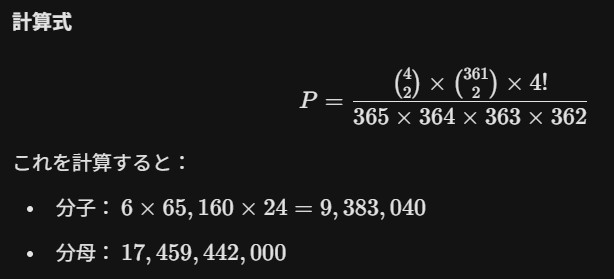
【0.0537%】
おお、かきぬまさんが調べたのとほぼ同じだ！その差約0.01％はほぼ誤差の範囲だろう。
0.0537%からいくと、1862組の4人グループが存在して始めて1組の2人同じ誕生日のペアを持つことになるわけだ。
ミラクル！
関連記事
書き手
田畠隆志
神奈川県横浜市／48歳
©30YEARS ARCADE
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
